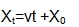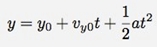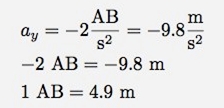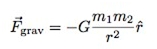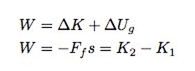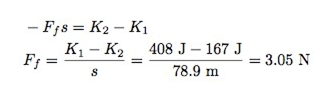今年3月底，游戏巨头Rovio发布了《愤怒的小鸟》的最新版本。在资料片中，天空突然出现了一个紫红色的漩涡，一只巨大的机械手从漩涡中伸出，抢走了小鸟们精心呵护的蛋蛋。愤怒的小鸟们为了夺回自己蛋，跃进漩涡。这个漩涡其实是一个通向太空的时空隧道。它们在太空中与绿色小猪展开了新的战斗。

在这个游戏中，一个有趣的设定是作为主战场的小星球外围有一个透明球壳，我们估且称其为结界。在结界外，小鸟直线飞行，不受任何引力和阻力。但是一旦进入结界内，星球立刻对小鸟产生强大的引力，改变它的运行轨迹。这个轨迹通常是椭圆形的，并且小鸟最终将会落到陨石表面。这一回，小鸟的战场环境怎么样？它们为什么会飞出这样一个奇葩的轨迹？一位美国物理学家尝试做了解答，今天我们就把他的分析方法介绍给大家。

【iOS用户点此播放】

物理学家的分析

美国物理学家Rhett Allain可以称得上是一个“愤怒的小鸟”专家了，当然这不是说他游戏打得特别好，而是指他通过对游戏进行数值分析，推导出了很多游戏的参数。这些参数对通关也许没有太大帮助，但却能够帮助玩家了解这些可爱的小鸟、小猪们的生活环境。迄今为止，他已经写了8篇关于愤怒的小鸟的 研究报告 ，帮助我们了解了弹弓的高度、小鸟的直径、各种不同小鸟的飞行特性等等。Rhett使用了一款免费的视频分析软件Tracker Video Analysis计算出小鸟运动的速度、加速度等物理参数。这款软件能够追踪视频中的图像元素，并对它们的运动进行建模。最近他也很及时地完成了太空版的初步分析，初步破解了小鸟圆周运动轨迹的秘密。在介绍 Rhett 对太空版的分析前，我们先以他求解弹弓尺寸为例介绍一下基本的分析方法和思路。
这个计算依据的是地面的版本，但是我们不知道任何一个物体的尺寸，因此先如下图所示，假定弹弓的高度为1 AB。

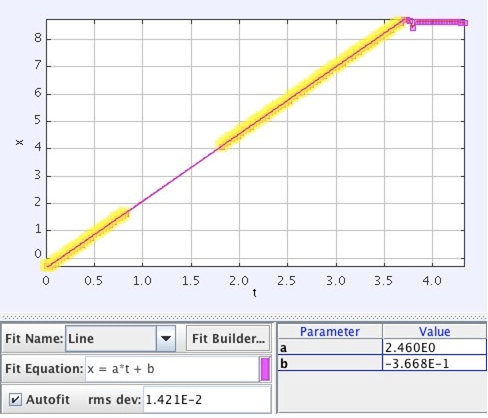
使用软件Tracker我们可以获得小鸟弹射出去之后的横坐标位置与时间关系：一条直线，这说明在游戏中小鸟做的是匀速运动。假设视频的播放时间和小鸟世界中的时间是一致的，根据

对这个直线进行拟合，很容易得到小鸟的速度为2.46AB/秒。

另一方面，初中物理告诉我们位置与速度和加速度的关系为：

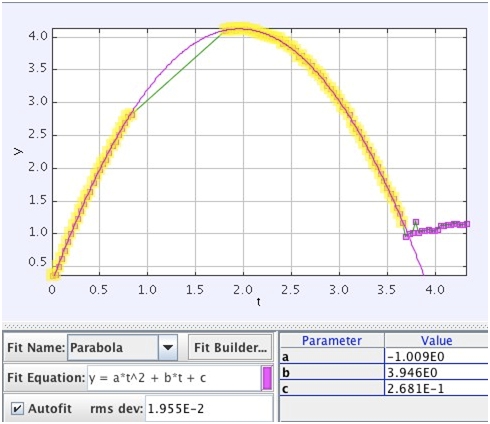
从 y 轴上的位置来看，我们可以获得如下图所示的抛物线。同时将上面的公式作为拟合的对象，求解y方向上的加速度可得：

图中拟合结果中的a就是加速度的一半，因此y方向的加速度-2 AB/ 秒-2。假设这个场景发生在地球上（重力加速度为9.8米/秒2）,通过下面的简单运算我们就可以求出AB的大小。

可见这是个大约有5米高的巨型弹弓，根据比例从图上测算出小鸟的尺寸可达到70厘米。所以其实游戏应该改名叫做“愤怒的大鸟”。

太空中的轨迹

回到最初的问题上，现在我们进入太空，看看结界里面到底发生了什么。从小鸟的飞行轨迹来看，星球对它会产生引力。万有引力定律告诉我们任意两个质点有通过连心线方向上的力相互吸引。该引力的大小与它们的质量乘积成正比，与它们距离的平方成反比，它与两物体的化学本质或物理状态以及中介物质无关。这段话可以通过下面的公式表达出来：

其中Fgrav为两个物体之间的引力，G为万有引力常数，m 1 、m 2分别为物体1和物体2的质量， r为两个物体之间的距离。不过这个公式不能直接用在拟合中，因为引力是有方向性的，在运动的过程中，引力的方向一直在发生变化， tracker程序无法处理这样的情况。

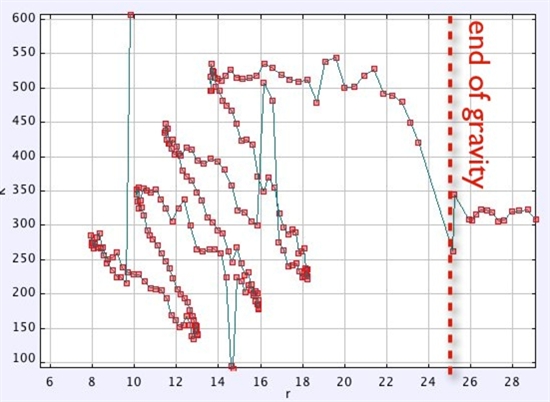
假定小鸟重量为1公斤，我们可以根据视频测量出小鸟的速度以及它相对于星球质心的距离r，从而得到动能值与r的关系如图所示。红色虚线的右边，小鸟在结界之外，速度保持一定，进入结界后， 受到引力的影响，它的速度发生周期性的变化。这里请忽略那些“毛刺”，它们是视频帧率不够稳定引起的。

从上面这张图中我们可以看到，在相同的高度，动能值可能不同，这说明结界内是有空气摩擦力的。这一点从小鸟最终一定会落到星体上以及星体上长着花花草草也可以看出。

使用tracker在视频中选取一段轨迹如下图:

当小鸟两次经过相同的高度，空气摩擦力做的功将等于动能的变化值:

路径的长度可以通过计算蓝色所包含的像素值求出。在起点求得动能为408焦耳，终点为167焦耳，距离78.9米，通过以下公式

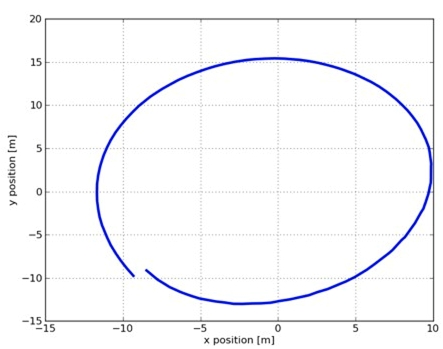
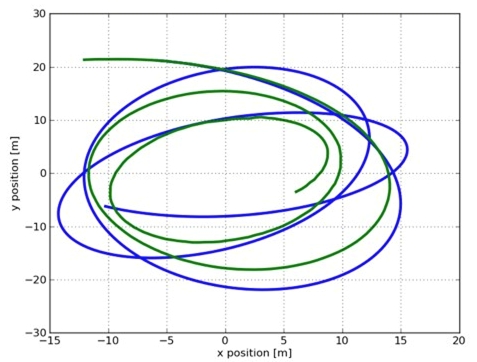
可以求得摩擦力大约是3.05牛顿。为了求得重力的大小， Rhett用VPython编程语言重建了结界内的场景。他设定小鸟的初始速度、星球的大小、摩擦力的大小等参数都与截取的游戏录像片段中一致。下图为一个模拟的路径。

通过改变同重力的大小，他可以将“模拟小鸟”的运动轨迹（下图中的蓝线）尽可能符合游戏录像中小鸟轨迹（下图中的绿线）。

根据以上的分析，Rhett最终得到以下这些结论：

只有有空气的地方才有重力（和摩擦力）。

重力系数为65牛/千克（地球表面的仅为9.8牛/千克）。

游戏中的重力系数似乎和小鸟与星球之间的距离无关，是一个常数。

摩擦力始终与运动反向相反等于定值3.05牛。

小鸟的初速度大约为25 米/秒（地球版本的约为23米/秒）。

以上的算法并不一定是最佳的，不过计算的思路确实很有意思。感兴趣的朋友们不妨下载软件，为了那些勇敢的小鸟们挺身而出，自己来试试看吧。（文/果壳网）